Extraction des bases génériques informatives de règles sans calcul de fermetures

précédent sommaire suivant

1.3 Analyse formelle de concepts

1.3.1 Introduction

Une base de donnees, appelee aussi contexte d'extraction ou d'une maniere generale contexte formel, est generalement representee par une relation binaire entre un ensemble d'attributs I et un ensemble d'objet O.

Definition 1 Contexte formel

Un contexte formel est un triplet K = (O,I,R), decrivant deux ensembles finis O et I et une relation (d'incidence) binaire, R, entre O et I tel que R ? O × I. L'ensemble O est habituellement appele ensemble d'objets (ou transactions) et I est appele ensemble d'attributs (ou items). Cha que couple (o,i) ? R designe que l'objet o ? O possede l'attribut

i ? I (note oRi).

Un exemple de contexte formel K est illustre dans la figure 1.1, avec O = {1,2,3,4,5} et

I = {A, B,C, D, E}.

FIG . 1.1 - Exemple de contexte formel

L'analyse formelle de concepts, introduite par Wille en 1982 [66], traite des concepts formels : un concept formel est un ensemble d'objets, l'extension, auxquels s'appliquent un ensemble d'attributs, l'intention. L'analyse formelle de concepts offre alors un outil de classification et d'analyse, dont la notion centrale est le treillis de concepts. Le treillis de concepts peut etre vu comme un regroupement conceptuel et hierarchique d'objets (a travers les extensions du treillis), et interprete comme une representation de toutes les implications entre les items (a travers les intentions) [58].

L'analyse formelle de concepts permet aussi de reduire considerablement le nombre de relations entre ensembles d'attributs, en ne generant que celles considerees comme non redondantes.

Dans ce qui suit, nous allons presenter les elements fondamentaux de l'analyse formelle de concepts.

1.3.2 Notion d'ordre partiel

- Ensembles ordonnes :

Soit E un ensemble. Un ordre partiel sur l'ensemble E est une relation binaire = sur les elements de E, tel que pour x, y, z ? E nous avons les proprietes suivantes [21] :

1. Reflexiyite : x = x

2. Anti-symetrie : x = y et y = x x = y

3. Transitiyite : x = y et y = z x = z

Un ensemble E dote d'une relation d'ordre =, note (E,=), est appele ensemble partiellement ordonne [21].

Soient P et Q deux ensembles partiellement ordonnes. Nous dirons que P et Q sont ordre-isomorphes, note P ~= Q, s'il existe une bijection f : P Q et tel que x = y dans P si et seulement si f(x) = f(y) dans Q. La bijection f est ainsi dite ordreisomorphisme [21].

- Relation de couverture :

Soient E un ensemble ordonne (E,= ) et x, y deux elements de E. La relation de couverture entre les elements de E, notee ?, est definie par x ? y si et seulement si x = y et tel qu'il n'existe pas d'element z ? E tel que x = z = y pour z =~ x et z =~ y.

Si x ? y, nous disons que y couvre x ou bien que y est un successeur immediat de x (et donc x est couvert par y ou x est un predecesseur immediat de y) [21].

- Join et Meet :

Soit un sous-ensemble S ? E de l'ensemble partiellement ordonne (E,=). Un element

u ? E est un majorant, ou borne-sup, de S si pour tout element s ? S, nous avons s = u. L'ensemble des majorants de S est note UB(S). D'une maniere duale, un element

ü ? E est un minorant, ou borne-inf, de S si pour tout element s ? S, nous avons v = s. L'ensemble des minorants de S est note LB(S) [27].

UB(S) = {u ? E | ?s ? S, s = u}
LB(S) = {v ? E | ?s ? S, v = s}

Le plus petit majorant d'un ensemble S, s'il existe, est le plus petit element de l'ensemble UB(S) des majorants de S. Cet element est note Join(S) (?S). D'une maniere duale, le plus grand minorant d'un ensemble S, s'il existe, est le plus grand element de l'ensemble LB(S) des minorants de S. Cet element est note Meet(S) (?S) [27].

h i

e

a b

c

f g

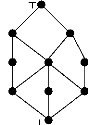
FIG . 1.2 -- Join - Meet

Exemple 1 Soit le treillis de concepts illustre par la figure 1.2. Ainsi, nous avons : UB({a,b}) = {T, h,i, f}

LB({e, f}) = {a, ?}

- Treillis complet : Un ensemble partiellement ordonne (E,=) non vide est un treillis si pour tout couple d'elements (x, y) ? E, l'ensemble {x, y} possede un plus petit majorant, note x ? y, et un plus grand minorant, note x ? y.

L'ensemble partiellement ordonne (E,=) est un treillis complet si pour tout sous-ensemble S ?E, les elements Join(S) et Meet(S) existent [21].

Les treillis sont frequemment representes sous forme d'un diagramme de Hasse (les arcs transitifs sont omis), appele egalement graphe de couverture [21]. Dans ce type de graphe, les sommets correspondent aux elements de l'ensemble E et les arcs aux relations de couverture entre les sommets [21].

Theoreme 1 Theoreme fondamental de l'analyse formelle de concepts [27] : L'ensemble des concepts formels, extrait a partir d'un contexte formel, constitue un treillis complet quand les concepts formels sont ordonnes par inclusion des extensions (ou par inclusion des intentions).

- Join-irreductible et Meet-irreductible :

Pour un element l d'un treillis complet L, nous definissons [21] :

l_* = ?{x ? L|x < l}
l* = ?{x ? L|l < x}

Un element l est dit Join-irreductible s'il couvre un element unique. D'une maniere duale, l est dit Meet-irreductible, s'il est couvert par un seul element.

L'ensemble des elements Join-irreductible de L est note par J (L) et l'ensemble des elements Meet-irreductible de L est note par M(L). Chacun de ces ensembles herite de la relation d'ordre de L [21].

Exemple 2 Dans la figure 1.2, b est un element Meet-irreductible, alors que e est un
element Join-irreductible. Dans la figure 1.3, nous avons J(L) = {b, c} et M(L) = {e, f}.

b c

a

d

e f

FIG 1.3 -- Join-irreductible - Meet-irreductible