I.5 Eléments de neurologie
L'émission des sons est un phénomène
bulbaire mais le contrôle des sons est d'origine corticale23.
Les centres corticaux, bilatéraux, sont reliés aux noyaux
bulbaires par les faisceaux géniculés. Les noyaux bulbaires
reçoivent des fibres des centres corticaux homolatéraux et
controlatéraux. La voix est donc une commande bilatérale,
à prédominance controlatérale.
22 Le Huche F., Allali A. (1978), p107, Op. cit. p12.
23 Le larynx est représenté dans la région
inférieure de la circonvolution frontale ascendante.
Etant donné le nombre de structures participant
à la phonation, de nombreux nerfs crâniens entrent en jeu pour la
production de la voix. Sans même aborder les phénomènes
neurologiques liés à la réalisation de la parole, et sans
détailler les multiples rôles de ces nerfs, notons l'importance
des nerfs V (langue, masseter, ptérygoïdiens, temporal, ...), VII
(lèvres, joues, muscles faciaux), IX, X (larynx, diaphragme, ...), XI
(pharynx) et XII (motricité de la langue).
I.6 Deux modèles de vibration des cordes
vocales
I.6.1 Les modèles linéaires de
vibration
Tous les modèles et théories de ce paragraphe
décrivent la vibration des cordes vocales de manière
linéaire, chacun apportant un éclairage différent sur les
modes de vibrations des cordes vocales.
I.6.1.1 La théorie
myo-élastique
Pour que les cordes vocales entrent en vibration, il faut dans
un premier temps qu'elles viennent au contact l'une de l'autre (cf
mécanismesd'accolement des CV I,1,5).
Les points d'insertions aryténoïdiens ainsi
fixés, les plis vocaux commencent à vibrer sous la pression de
l'air expiratoire. Chaque cycle vibratoire équivaut à la
succession d'une adduction et d'une abduction des plis vocaux. Pour la
production d'un son grave, l'ouverture débute par la partie
inférieure des plis pour se propager dans un mouvement allant vers le
haut et le dehors. Ensuite, la fermeture glottique débute
également par la partie inférieure des plis. Il existe donc une
différence de phase sur le plan vertical puisque les plis vocaux ne
s'accolent pas sur toute leur hauteur en un mouvement. Les mécanismes
vibratoires de la production de sons aigus sont semblables, en dehors du fait
que la tension des ligaments et des muscles vocaux supprime la
différence verticale de phase.
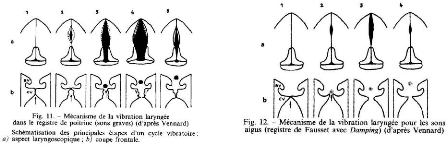
Schématisation des mécanismes laryngés
24
I.6.1.2 La théorie myo-élastique
aérodynamique
La vibration laryngée dépend donc de la
contraction des muscles qui assurent la fermeture glottique d'une part, et de
la pression de l'air expiratoire qui tend à écarter les cordes
vocales d'autre part. Mais cette oscillation libre doit être entretenue
régulièrement sans quoi elle s'arrêterait progressivement
faute d'apport d'énergie25. C'est pourquoi il est apparu
nécessaire aux chercheurs d'ajouter une troisième force au
modèle:
-force de rappel qui entretient l'oscillation en accolant
à nouveau les cordes vocales lorsqu'elles ont été
éloignées du fait de la pression sous-glottique
-force de synchronisation qui fait en sorte que l'oscillation
libre ne soit pas perturbée à chaque début de cycle par
l'énergie d'entretien.
L'effet Bernoulli, ou effet de rétro-aspiration, plus
communément appelé effet de succion, conjugue les deux
critères ci-dessus. Comme il a été signalé, lors
d'un cycle vibratoire, les muqueuses des cordes vocales sont
écartées sous l'effet de la pression sous-glottique
(c'est-à-dire qu'elles sont comprimées comme des ressorts). Il se
crée alors une pression négative entre les cordes vocales lors du
passage de l'air à grande vitesse. Cette pression négative aspire
les muqueuses l'une vers l'autre. Revenues à leur position
médiale de départ (tout comme des ressorts retrouveraient leur
position initiale), elles peuvent à nouveau être
éloignées par la force de pression sous-glottique et ainsi de
suite. En définitive, l'effet Bernouilli permet donc l'autoentretien de
la vibration sans pour autant perturber cette dernière.
24 Cornut G, p22-23, Op. cit. p8.
25 De la même manière un enfant sur une
balançoire a besoin d'être poussé
régulièrement sans quoi le mouvement oscillatoire
s'arrêterait.
I.6.1.3 Les modèles de la masse
vibrante
La théorie myo-élastique aérodynamique
dit modèle à << une masse » a été
développée par Van Den Berg. La hauteur du son laryngé y
est fonction des caractéristiques de masse et de tension des cordes
vocales et répond à l'équation:
F0 = ( 1/ 2ð ) v (k/m) , où -F0 est la
fréquence fondamentale
-k est la tension des cordes vocales -m est la masse des cordes
vocales.
Nous pouvons en déduire que plus la masse vibrante est
élevée plus le son sera grave et inversement. Et plus la tension
sera élevée plus le son sera aigu et inversement.
Les modèles à deux masses de Ishisaka et
Flanagan, et celui à trois masses de Titze prennent en compte les
différences de masses entre les cinq couches des plis vocaux.
Malgré cela, tous ces modèles répondent au même
principe de base: lors de l'échange d'énergie entre l'air
pulmonaire et la muqueuse cordale, la fréquence de l'oscillation
dépend uniquement des caractéristiques de la corde.
I.6.1.4 Le modèle des oscillations à
relaxation
En somme, le son laryngé résulte d'une
alternance de mouvements plus ou moins brusques d'ouvertures et de fermetures
glottiques. Ce mécanisme est couramment assimilé à un
oscillateur << à relaxation ». En d'autres termes à
chaque ouverture glottique l'air est relâché par <<
bouffées » ou << puffs »26. Le son
laryngé, qui sonne continu à notre oreille, est donc
consitué d'une série de << puffs » d'air assimilables,
en définitive, à des impulsions acoustiques. Le rythme,
l'amplitude et la forme des impulsions dépendent de l'énergie
introduite par la pression sous-glottique et de l'élasticité des
cordes vocales, et déterminent respectivement la fréquence,
l'intensité et le timbre du son laryngé.
26 Comme lorsqu'un récipient se remplit d'eau jusqu'au
siphon et qu'une seule goutte suffit à le vider. Il y a donc
accumulation puis relaxation ce qui transforme l'énergie continue en
énergie alternative.
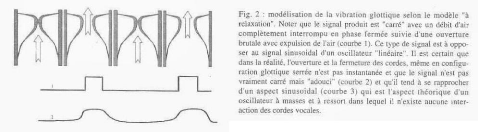
Modèle de la vibration glottique à relaxation
27
I.6.2 Un modèle non linéaire de la
vibration
glottique28
I.6.2.1 Limites des modèles
linéaires
Tous les modèles ci-dessus décrivent les
mécanismes linéaires de la production du son laryngé.
Aussi ont-ils ce défaut de décrire les mouvements des cordes
vocales sans prendre en compte le fait que ces mouvements puissent être
modifiés par le contact des plis vocaux. Or la trajectoire de chaque
corde vocale est nécessairement modifiée par son contact avec la
corde controlatérale. Et, tout comme les deux moitiés du visage
sont différentes, les deux cordes vocales ne sont pas en tout point
identiques. Aussi, les deux cordes vocales ne peuvent pas vibrer à la
même fréquence.
Par ailleurs, l'effet de Bernouilli est dit linéaire
puisque proportionnel à la vitesse de l'air. Mais il est possible de le
considérer comme un phénomène non linéaire
puisqu'il ne se déclenche qu'à partir d'un certain seuil de
pression phonatoire. Ce seuil est dépendant de
-la raideur et la viscosité de la masse cordale (plus
la tension de la corde et sa viscosité sont importantes et plus le seuil
de pression sous-glottique doit augmenter)
-la largeur de la fente glottique pré-phonatoire (plus
la fente est large, plus l'air s'écoule, nécessitant ainsi une
augmentation de la pression sousglottique)
27 Giovanni A., Ouakine M., Garrel L., Ayache S., Robert D,
(2002), « Un modèle non-linéraire de la vibration glottique.
Implications cliniques potentielles », Rev. Laryngol. Otol.
Rhinol., 123;5; 273-277, p176.
28 Ibid.
-la différence de pression transglottique (une pression
sus-glottique élévée nécessite une pression
sous-glottique encore plus élevée)
De même que la trajectoire de chaque corde est
différente, nous pouvons donc avancer que l'effet Bernouilli est lui
aussi un phénomène non linéaire. Les théories
basées sur les principes myo-élastiques ne sont donc pas
suffisantes à elles seules pour décrire tous les
phénomènes vibratoires.
I.6.2.2 Le modèle slip-stick
Les chercheurs ont donc émis l'hypothèse que
chaque corde vocale vibrerait selon ses propres modalités
fréquentielles. Et lorsque les deux cordes vocales se rencontrent, une
synchronisation de leur fréquence s'opèrerait. En couplant les
dimensions verticale et horizontale de la vibration glottique lors
d'expériences sur des larynx excisés, les chercheurs ont pu
vérifier leurs hypothèses.
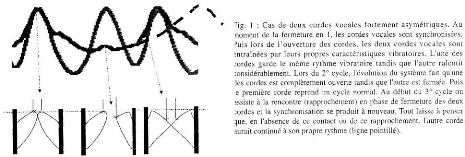
Synchronisation de la vibration glottique
29
Les principaux facteurs de synchronisation entre les cordes
vocales sont:
-les relatives similitudes de forme et de tension des deux
cordes à
l'état normal
-la mise en contact d'une partie de la masse vibrante des
deux
cordes vocales
-la viscosité du mucus30.
29 Giovanni A., Ouakine M., Garrel L., Ayache S., Robert D,
(2002), p275, Op. cit. p27.
30 Plus le mucus est visqueux, plus la fréquence
vibratoire diminue et plus le seuil de phonation est élevé: en
effet plus le mucus est visqueux et plus le temps d'adduction est
augmenté. Il y a donc des relations complexes entre qualité du
mucus, fréquence et amplitude vibratoires.
Ces recherches ont abouti à la création d'un
nouveau modèle de vibration glottique: le modèle «
slip-stick » ou « glissé-collé » en
français. Les auteurs comparent ce modèle au fonctionnement d'un
archet sur une corde de violon. Au début de la vibration, l'archet tire
la corde hors de sa position d'équilibre. Pendant un premier temps, les
forces élastiques s'opposent à ce mouvement. Puis les forces de
rappel deviennent plus importantes que la force d'adhésion. La corde se
« décolle » alors de l'archet et oscille librement.
Lorsqu'elle a suffisamment dissipé d'énergie, elle peut à
nouveau être « collée » par l'archet (sous l'effet de
Bernouilli). Par conséquent, la phase forcée pendant laquelle la
corde vibre de la même façon que l'archet, est suivie d'une phase
libre durant laquelle la corde vibre à sa propre fréquence.
L'archet joue donc à la fois le rôle de l'effet Bernouilli et
celui de contact avec la corde controlatérale31.
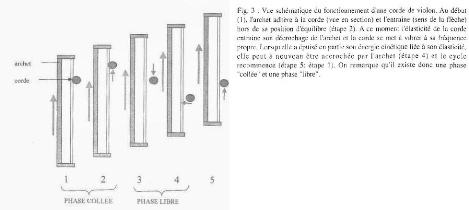
Schématisation du modèle slip-stick
32
En résumé, lors d'un cycle normal, les deux
cordes n'étant pas exactement identiques, elles devraient vibrer
différemment. Mais la partie « collée » du cycle
synchronise leurs vibrations en mettant en contact leurs masses vibrantes. Les
auteurs considèrent que tant que les deux cordes ne diffèrent pas
outre mesures d'un point de vue anatomique, ce mécanisme «
slip-stick » fonctionne33.
31 De même, les auteurs comparent la viscosité du
mucus des cordes vocales à la collophane déposée sur
l'archet par les violonistes.
32 Giovanni A., Ouakine M., Garrel L., Ayache S., Robert D,
(2002), p276, Op. cit. p27.
33 Il est intéressant de noter qu'une voix bitonale
résulte d'une synchronisation vibratoire d'un cycle sur deux.
Par ailleurs, le mode de fonctionnement idéal serait
atteint pour une tension et une longueur identiques pour chaque corde vocale.
Il ne nécessiterait donc presqu'aucun processus de synchronisation. Par
conséquent, la phase « libre » s'en trouverait
augmentée. A l'inverse, plus les cordes vocales seraient
asymétriques et plus la phase « collée » se devrait
d'être importante pour assurer la synchronisation. Le mécanisme
d'augmentation du volume dans le forçage vocal apparaît ici comme
très voisin du mécanisme de compensation des anomalies
vibratoires.
| 


