Une description de differentes options exotiques à partir du modèle de Cox Ross et Rubinstein sur quelques periodes

2 Le modèle sur une période

Nous définissons un marché financier composé de deux actifs dont le prix à la date t est noté :

avec 0 < t < T l'actif risqué l'actif non risqué

St Rt

L'actif risqué peut prendre deux valeurs S à la fin de la période soit il est multiplié par u soit par d tel que S0 <uS0 et S0 > dS0. On a une première propriété implicite : u> 1 et d < 1. On représente ce modèle sous forme d'arbre binaire, du fait des deux valeurs prises par l'accroissement de l'actif. On note Q la probabilité historique telle que l'actif a un prix qui augmente avec la probabilité q et un prix qui diminue avec la probabilité (1 - q). On notera S0 = S. Sous forme d'arbre on a donc :

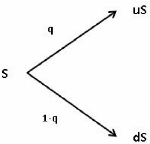
FIG. 1 - Arbre binomial à une période

Nous allons tout d'abord définir une condition fondamentale que le modèledoit respecc ter : l'absence d'opportunité d'arbitrage, c'est à dire que

u>1+r>d

Définition 1. On appelle univers risque neutre, une économie oùles agents sont en moyenne indi~érents entre gagnerdel'argent ssirement (placement enanque auauu sans risque r) ou le jouer avec du risque (acheter des actions risquéesetc..).

Proposition 1. la probabilité de hausse dansl'univers risque au neutreest

r+ 1--d

p=
	u--d

preuve : Si un actif vaut S à la date initiale, à la date t = 1 sa valeur espérée est pour une probabilité p :

E[S1] =p.uS+(1 --p)dS

Dans l'univers que l'on veut créer cette espérance doit avoir la même valeur que si l'on avait placé la valeur de l'actif au taux sans risque r. Soit :

E[S1] = (1+r)S

p.uS+(1--p)dS= (1+r)S

r+1--d

p=
		u--d
1--p= 1			r+1--d			u--(1+r)
			u--d			u--d

etdonc0<p< 1'~d< 1+r<u

La condition u > 1 + r > d est donc equivalente à l'existence d'une probabilité risque neutre. Sous cette probabilité les agents sont neutres au risque, nous allons doncdans la suite calculer toutes les espérances sous cette probabilité P. 7

3 Le modèle sur T périodes

On généralise le modèle à une période en considérant que le marché financier peut se dupliquer aux instants t = [0, 1, ..., T]. L'actif non risqué évolue toujours au taux constant r entre deux périodes de temps [t,t + 1]. On le note au temps t

Rt=(1+r)^t

L'actif risqué prend deux valeurs à chaque période detempstelles que

? ????? ?????

Su t+1 = u.St Sd t+1 = d.St

Sur l'arbre suivant nous pouvons observer lensemble des probabilités en rouge et des valeurs du sous jacent en noir sur trois périodesChaque probabilité est celle datteindre la valeur du sous jacent.

uuuS

ppp

uuS pp

uS

uudS

p

3pp(1 -p)

S		udS
1		2(1 -p)(1-p)

dS

1-p

uddS

3p(1-p)(1-p)

On peut généraliser et dire que sur T périodes la valeur SuhdT ^-h atteinte par ST cor-

ddS

(1-p)(1 -p)

FIG. 2 Arbre binomial à trois périodes

St+1 - St St+1 = Stît+1 ? = ît+1- 1 ? St

? ????? ?????

u-1 >0 d-1 <0

respond à une trajectoire dont la probabilité est p^h(1 - p)^T_h. Si l'on fait l'hypothèse que

_(T )

ces mouvements, à la hausse ou à la baisse sont indépendants, il y a exactement h trajectoires qui atteignent cette valeurLes T + 1 valeurs SuhdT _^h, h = 0, ..., T que peut prendre ST sont les T + 1 valeurs possibles d'une variable aléatoire deloi binomiale donnée par :

( _(T )

ST = SuhdT _h)

i = (p^h)(1 - p)^T_h

h

Soit ît E Q = {u,d} tel que :

St+1 = S0î1î2...ît+1

la loi de probabilité de ît est :

i (ît =u)= 1-i (ît =d)=p

La filtration naturelle associée représente l'information accumulée sur les prix de lactif risqué jusqu'à t , on la note :

(Ft)t<T = a{S0, S1, S2, S3, ...St}

Une hausse ou baisse est en fait celle du taux de rendement de lactif qui par hypothèse est de variance historique a² et de moyenne u par unité de temps. Ces variations sont telles que ?t E {0, .., T} et ?ît E {d, u}

autrement dit sil'on ne peut pas gagnerde l'argent àpartir de rien.

En effet, par exemple, si r + 1 > u, alors le taux sans risque rapporte plus quun actif risqué : à t = 0 on vend le sous-jacent S et on place la somme acquise au taux sans risque. On rachète à t = T le même sous jacent. La somme sans risque ayant évolué plus vite que l'actif risqué, à terme la différence entre ce que lon a vendu et rachetésera positive, on aura gagné de l'argent sans en investir.

Proposition 2. Un marché financier est viable si et seulement s'il eeiste une probabilité P* équivalente à Q , la probabilité historique, pourlaquelle le cours actualisé des actiis ((St) 0 t T) est une martingale, c'est à dire St

(1+r)t est une martingale

Démonstration : Rappelons que Mt est une martingale sous P^* si

Ejp*[Mt+1 | Ft] = Mt

Par hypothèse l'information acquise sur les prix du sous jacent jusque t n'influe pas sur ce qui se passe en t + 1 et _ît+1 est indépendant de Ft.

Alors Mt = St

(1+r)t est une martingale sous P^* si Ejp*[Mt+1 | Ft] = Mt.

[ St+1 1 = Ejp^*[Stît+1 | Ft]

Or : Ejp* (1 + r)t+1 | ^Ft(1 + r)^t+1

St

(1+r)t+1 Ejp*[ît+1 | Ft]

(1 + r)t+1 [p^*u + (1 - p^*) d]

St

= Mt [p^*u + (1 -p^*)d]

(1+ r)

et donc la condition à remplir est :

up^*+(1--p^*)d= 1+r

u.p^* + d.(1 -- p^*) =1 1+r

	1+ r--d		= p*
	u--d

On en déduit que la probabilité risque neutre P est la seule probabilité pour laquelle le prix du sous jacent actualisé est une martingale et doncla seule probabilité pour laquelle il n'existe pas d'opportunité d'arbitrageP^* est une probabilité si et seulement si :

0<

1+r--d

=p^*<1

u--d

?

?????

?????

Les inégalités sont strictes puisque que lon veut quily ait durisque.Or

p* > 0 1+ r > d

p* <1 1+ r < u

On en déduit que si l'action prend deux valeurs distinctes à chaque noeud

0<d<1+r<u

Une condition pour que le marché soit viable est donc r ?]d -- 1; u -- 1[, la probabilité risque neutre P est donc la seule probabilité pour laquelle le prix du sous jacent actualisé au taux sans risque est une martingaleDansla suite les espérances seront calculées sous cette probabilité risque neutre.