II.2.2 Analyse de stationnarité
Afin d'analyser la stationnarité des séries
étudiées nous appliquons le test de racine unitaire Dickey-Fuller
Augmente (ADF).C'est un test dont l'hypothèse nulle est la non
stationnarité et qui permet de prendre en compte
l'auto-corrélation possible de la série
différenciée via une correction utilisant les valeurs
retardées. En général l'équation du test est la
suivante : 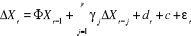
Avec 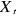 est la
série, est la
série, 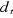 la
tendance, la
tendance, 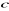 la constante, la constante,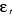 terme
aléatoire et p le nombre de retard. Ce dernier est
déterminé à partir des auto-corrélations partielles
de terme
aléatoire et p le nombre de retard. Ce dernier est
déterminé à partir des auto-corrélations partielles
de 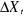 ; on retient le retard correspondant à la dernière
auto-corrélation significative. ; on retient le retard correspondant à la dernière
auto-corrélation significative.
Tout d'abord, on estime le modèle par le MCO avec
tendance et constante. Puis on teste la significativité de la tendance,
si elle est non significative, on estime le modèle avec constante
seulement. Si la constante n'est pas significative, on estime le modèle
sans tendance ni constante. Enfin on compare la statistique du test ADF avec la
valeur critique. Si la statistique du test est supérieure à la
valeur critique alors on accepte H0 c'est-à-dire la non
stationnarité de série.
a) Analyse de stationnarité des
séries pour la première période
Les résultats du test ADF pour les séries LWTI,
DLWTI, LIMS et DLIMS sont présentées dans le tableau
ci-dessous :
Tableau3 : Test de racines unitaires sur les séries
pour la période1
|
Séries
|
trend
|
intercept
|
Nombre de retard
|
t-statistic
|
Critical value (5%)
|
Stationnaire ou non stationnaire
|
|
LWTI
|
non
|
non
|
0
|
0.980691
|
-1.945987
|
Non stationnaire
|
|
DLWTI*
|
non
|
non
|
2
|
-6.687676
|
-1.946072
|
Stationnaire
|
|
LIMS
|
non
|
oui
|
1
|
-2.780963
|
-2.908420
|
Non stationnaire
|
|
DLIMS**
|
non
|
non
|
3
|
-13.13276
|
-1.946072
|
Stationnaire
|
* DLWTI : la série LWTI en différence
première.
**DLIMS : la série LIMS en différence
première.
Pour la série LWTI, on a estimé le modèle
par la méthode de MCO avec constante et tendance et on a trouvé
quelles ne sont pas significatives. Pour cela, on a adopté le
modèle sans tendance ni constante. Il est bien claire que la statistique
du test est supérieure à la valeur critique au seuil de 5% donc
on accepte l'hypothèse nulle du test ADF qui est la non
stationnarité du série LWTI.
Passant à l'étude de stationnarité de la
série en différence première(DLWTI). De même, le
modèle significatif est celui sans tendance ni constante. La statistique
du test est inférieure à la valeur critique ce qui signifie le
rejet de l'hypothèse nulle et donc la série DLWTI est
stationnaire. Par conclusion, la série LWTI est intégrée
d'ordre 1 (LWTI~>I(1)).
Concernant la série LIMS, on a adopté le
modèle sans tendance et avec constante. La statistique du test est
supérieure à la valeur critique au seuil de 5% donc on accepte
l'hypothèse nulle du test ADF qui est la non stationnarité du
série LIMS. Pour la série DLIMS, on a adopté le
modèle sans tendance ni constante vérifiant la
stationnarité de la série. D'où LIMS est
intégrée d'ordre 1(LIMS~>I(1)).
b) Analyse de stationnarité des
séries pour la deuxième période
Les résultats du test ADF pour les séries LWTI,
DLWTI et LIMS sont présentées dans le tableau
ci-dessous :
Tableau4 : Test de racines unitaires sur les
séries pour la période2
|
Séries
|
trend
|
intercept
|
Nombre de retard
|
t-statistic
|
Critical value (5%)
|
Stationnaire ou non stationnaire
|
|
LWTI
|
oui
|
oui
|
2
|
-2.672735
|
-3.428198
|
Non stationnaire
|
|
DLWTI
|
non
|
oui
|
4
|
-11.98327
|
-2.873142
|
Stationnaire
|
|
LIMS
|
non
|
oui
|
4
|
-5.670426
|
-2.873093
|
stationnaire
|
Pour la série LWTI, on a adopté le modèle
avec constante et tendance. La statistique du test est supérieur
à la valeur critique ce qui implique la non stationnarité de la
série LWTI. Pour la série DLWTI, le modèle adopté
est celui avec constante et sans tendance et qui vérifie la
stationnarité de la série DLWTI. LWTI n'est pas stationnaire mais
la série en différence première est stationnaire donc LWTI
est intégrée d'ordre1 (LWTI~>I(1)).
Par contre, le résultat du test ADF, appliqué
sur le modèle avec constante et sans tendance de la série LIMS
implique que la série est stationnaire donc elle est
intégrée d'ordre 0(LWTI~>I(0)).
c) Analyse de stationnarité des séries
pour la troisième période
Les résultats du test ADF pour les séries LWTI,
DLWTI, LIMS et DLIMS sont présentées dans le tableau
ci-dessous :
Tableau5: Test de racines unitaires sur les séries pour
la période3
|
Séries
|
trend
|
intercept
|
Nombre de retard
|
t-statistic
|
Critical value (5%)
|
Stationnaire ou non stationnaire
|
|
LWTI
|
non
|
non
|
3
|
-1.026351
|
-1.945987
|
Non stationnaire
|
|
DLWTI
|
non
|
non
|
5
|
-7.285640
|
-1.946072
|
Stationnaire
|
|
LIMS
|
non
|
non
|
1
|
-0.636754
|
-1.946072
|
Non stationnaire
|
|
DLIMS
|
non
|
non
|
2
|
-13.68534
|
-1.946072
|
Stationnaire
|
Pour toutes les séries on a adopté le
modèle sans constante ni tendance.
Pour la série LWTI, la statistique du test est
supérieure à la valeur critique au seuil de 5% donc on accepte
l'hypothèse nulle du test ADF qui est la non stationnarité du
série LWTI. Passant à l'étude de stationnarité de
la série en différence première(DLWTI), la statistique du
test est inférieure à la valeur critique ce qui signifie le rejet
de l'hypothèse nulle et donc la série DLWTI est stationnaire. Par
conclusion, la série LWTI est intégrée d'ordre 1
(LWTI~>I(1)).
Les résultats sont de même pour la série
LIMS, en effet elle est intégrée d'ordre 1(LIMS~>I(1)).
| 


