III.9.1. Paramétrisation d'un bras manipulateur de
type série
A titre d'exemple, si on étudie un système
articulé évoluant dans un espace à trois dimensions en
considérant les positions et rotations, alors les coordonnées
généralisées seront au nombre minimal égal à
6.
Pour un manipulateur quelconque constitué de nb
corps rigides reliés en série par nb liaisons
rotoîdes et/ou prismatiques, nous avons, dans un vecteur qb
à nb coordonnées indépendantes.
|
qb
|
? 1
q 1
? ?
q
? ?
2
? ?
:
? ?
? ? ? ?
q n b
|
L'exemple choisi illustré en figure Fig.III.2
représente les différents paramètres nécessaires
à la description du mouvement du bras manipulateur, composé de
deux corps rigides de longueurs respectives a1 et a2 (non
nulles) et comportant deux liaisons rotoïdes. Ce bras comporte deux
degrés de libertés puisqu'il compte deux liaisons rotoïdes
aptes à effectuer des rotations indépendamment les unes aux
autres.
Les coordonnées généralisées sont
représentées dans le vecteur de configuration q =
[qb1 qb2]T (sachant que qb1
et qb2 sont les angles de rotation des deux
liaisons). La dimension de l'espace généralisé est
égale au nombre degré de liberté du système
dim(EGE)=í=2.
Le vecteur des coordonnées opérationnelles
A=[A1 A2 A3]T=[XOT YOT
Ø]T représente les coordonnées en position
XOT et YOT du point
OB2 dans le repère de la base du bras
RB0(OB0,xB0,yB0) ainsi que l'orientation Ø du
second corps dans le même repère ; la
dimension de cet espace opérationnel
dim(EOP)est égale à u=3, car c'est le
nombre de coordonnées opérationnelles du
système[Bay01].
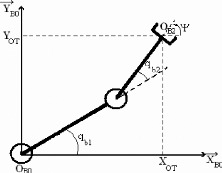
Fig.III.2 : Exemple de paramètrisation d'un bras
manipulateur à 2 degrés de liberté.
Le modèle géométrique direct du
système articulé est :
A1=a1Cos(qb1)+a2Cos(qb1+qb2) A
2=a 1Sin (qb1)+a2Sin (qb1+qb2)
Á3=qb1+qb2
Le modèle cinématique sera calculé en
dérivant les coordonnées opérationnelles, il en
résultera :
&
A a Sin q a Sin q q q a Sin q q q
1 1 1 2 1 2 1 2 1 2 2
= - + + - +
( ( ) ( )) ( )
& &
b b b b b b b
&
A a Cos q a Cos q q q a Cin q q q
2 1 1 2 1 2 2 2 1 2 2
= - + + + +
( ( ) ( )) ( )
& &
b b b b b b b
&
A q q
3 1 2
= +
& &
b b
La représentation matricielle de ce modèle est donc
:
E i E - + + - +
A ( a Sin( q ) a Sin( q q )) a Sin( q q )
&
? ? ? ? E i
1 1 b1 2 b1 b2 2 b1 b2 q &
& I b1
? ? = ? + + + I ?
A a Cos( q ) a Cos( q q ) a Cos( q q )
? ? ? ' L ]
2 1 b1 2 b1 b2 2 b1 b2 q &
& b2
? ? ?
A ? ?
1 1
3 1 3
Jb
Le degré de mobilité de ce bras manipulateur est
égal à Ddmb=2 vu qu'il n'y a pas de
contraintes non holonomes, il est de ce fait égal au degré de
liberté du système u=Ddmb=2.
Vu que notre système présente la
caractéristique í<u, cela implique que,
géométriquement, c'est un cas de figure considéré
comme impossible, alors que cinématiquement, il est sous actionné
(d'après le paragraphe III.7).
Nous allons considérer u=í
pour que le système ne soit plus sous actionné, cela nous
amène à paramétrer notre processus en modifiant le vecteur
des coordonnées opérationnelles, tel que A=[XOT
YOT]T en éliminant la composante de l'orientation,
de ce fait, ce bras est considéré comme non redondant
vis-à-vis de la tâche demandée car il possède deux
actionneurs.
Dans ce cas, la matrice Jacobienne devient :
- + + - +
( ( ) ( )) ( )
a Sin q a Sin q q a Sin q q l
1 1 2 1 2 2 1 2
b b b b b
J b = ? ?
? + + +
a Cos q a Cos q q a Cos q q
1 1 2 1 2 2 1 2
( ) ( ) ( )
b b b b b ÿ
Le déterminant de Jb vaut donc :
Det(Jb)=a1a2Sin(qb2)
En estimant l'expression de ce déterminant, nous
pourrons constater que si Det(Jb)=0, la configuration
correspondante est singulière ; dans le cas du bras
étudié, cela implique que qb2=0+ kð
(k? N). Cette condition nous permet de considérer que le
degré de liberté local
uddl est égal à 2 pour toutes les
configurations non singulières. Le degré de liberté global
u est égal également à 2.
Nous pourrons conclure que pour
qb=[qb1 0+kð(k?
N)]T (quel que soit qb1), le bras est en
singularité ; dans ce cas, le degré de liberté local
uddl décroît, il devient égal à
1 (uddl= 1). Par contre, le degré de liberté
global ne change jamais et reste toujours égal à 2.
Le bras peut être considéré comme redondant
géométriquement dans le cas où la situation de l'OT
est A=[XOT].
| 


