III.9.3. Etude d'un manipulateur mobile à roues
La configuration d'un manipulateur mobile à roues est
connue, dés lors que les configurations de la plateforme et du bras
manipulateur qui la composent sont connues.
Elle est définie sur un espace EGE
de dimension í=nb+np (nb
est la dimension de l'espace des configurations du bras et
np la dimension de l'espace des configurations de la
plateforme) par un vecteur q tel que :
? 1
q
q b
= ? ?
? ?
q p
Comme pour les bras manipulateurs, la situation d'un organe
terminal pour un manipulateur mobile est égale au minimum à 6,
dans un espace tridimensionnel.
Il est plus intéressant de choisir un bras manipulateur
tel que la taille de son espace opérationnel u soit
égale au nombre de coordonnées opérationnelles du
système complet.
Cela revient à considérer que si la plateforme est
amenée à ne pas bouger (selon la mission exigée), le
système sera tout de même apte à réaliser la
tâche désirée [Pad05].
Nous allons dans ce qui suit expliciter les notions
fondamentales pour une paramétrisation correcte du manipulateur mobile
à étudier. Le bras manipulateur considéré est de
type double pendule horizontal (les deux axes de rotations sont verticaux et
perpendiculaires au plan d'évolution de la plateforme RP
(Op, x p , y p
)
r r ) ; la plateforme quand à elle est de type voiture.
Chaque partie du robot résultant de la combinaison a été
présentée seule auparavant pour une
? q Ò
b 2
q ou
? ?
= X P
? ?
Y
? P Ò
? ? á J ?
? q b 1 1
1
1 Ò
?
?
?
?
?
?
?
?
J
qb
qb
2
? 1
? 2
?3
XP
YP
á
â3
meilleure compréhension. Le manipulateur mobile auquel
nous nous intéressons est présenté dans la figure
Fig.III.4 [Pad05]:
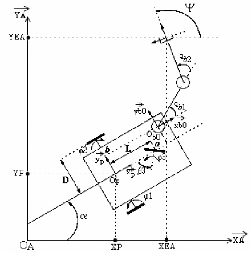
Fig.III.4 : Représentation d'un manipulateur
mobile plan
Dans le cadre de notre étude, le manipulateur mobile se
présente comme plan, et évoluant dans un espace à deux
dimensions, nous décrivons la situation de l'OT comme : A
=[A1 A2 A3]T=[XEA YEA Ø]T,
ces coordonnées opérationnelles seront toujours
considérées dans
RA= (OA ,x A ,
yA)
r r , elles spécifient les deux
coordonnées cartésiennes ainsi que l'orientation de l'OT
avec u=3 représentant la dimension de l'espace
opérationnel dim(EOP)=3.
En considérant les coordonnées
généralisées qb=[qb1 qb2]T du
bras manipulateur, et si nous ne nous intéressions qu'à la
situation qp=[XP YP á]T de la
plateforme (en omettant d'évoquer les rotations des différentes
roues), alors, le degrés de liberté du système
considéré estí=2+3=5 ; cette
représentation est aussi appelée configuration réduite du
système. Par contre, au cas où notre intérêt se
portait sur la configuration de la plateforme mobile
qp=[?1 ?2 ?3 XP YP á â3]T,
l'espace des configurations EGE serait donc de dimension
í=2+7=9.
Les différentes configurations envisagées pour le
système complet sont les suivantes [Bay01] :
Une ambiguïté peut se présenter dans le
fait d'utiliser la configuration ou la situation du système mobile, car,
pour considérer la configuration d'un système de manipulation
mobile, on peut ne considérer que la situation du système mobile
; elle peut être suffisante pour pouvoir identifier le système,
mais elle peut présenter des lacunes lors du passage à
l'étude de la commande. D'un point de vue purement
géométrique, la situation de la plateforme suffit pour identifier
le système de manipulation mobile dans le plan
RA=(OA,xrA, fIA), cela
transparaîtra plus clairement lors de la construction des
modèles géométriques comme suit.
·
Modèles géométriques
Pour notre système qui se présente comme plan, le
modèle géométrique direct est le suivant :
A1=XEA=
Xp+aCos(a)-bSin(a)+a1Cos(a+qb1)+a2Cos(a+qb1+qb2)
(3.23)
A2= YEA= Yp+
aSin(a)-bCos(a)+a1Sin(a+qb1)+a2Sin(a+qb1+qb2)
(3.24)
A3=Pr=qb1+ qb2+ a (3.25)
Il n'y a pas de lois particulières pour inverser le
modèle géométrique d'un manipulateur mobile.
Nous pouvons déjà certifier que le modèle
géométrique inverse comporte une infinité de solutions
puisqu'il présente une redondance géométrique ; cela
apparaît dans le fait que le nombre de coordonnées
généralisées soit supérieur au nombre de
coordonnées opérationnelles (v>p). L'ordre de cette
redondance géométrique est v--p=5-3=2.
Sachant que les coordonnées du point
Ob0 sont (a, b) dans le repère
Rp=(Op , xp , yp ) ; en
supposant que a=0 et b=0, et en
remplaçant (3.25) dans (3.24) et (3.23), elles se transformeront en :
A1=Xp+a1Cos(a+qb1)+a2Cos(A3)
A2= Yp+a1Sin(a+qb1)+a2Sin(A3) On
aurait donc :
A 1-Xp-a1Cos(A3)=
a1Cos(a+qb1) (3.26)
A2-Yp-a2Sin(A3)=a1Sin(a+qb1)
(3.27)
En faisant l'opération mathématique
((3.29)2+(3.30)2) on aura:
(A1-a2Cos(A3)-Xp)2+(A2-a2Sin(A3)-Yp)2=a1
2 (3.28)
Cette expression représente une contrainte par rapport
à certaines coordonnées
généralisées,
puisque le choix des deux
coordonnées Xp et Yp doivent la satisfaire
; ainsi, en fixant Xp, on
peut déduire YP. D'autre part, les
coordonnées généralisées á et
qb1 présentent une infinité de solutions, puisque dans
les expressions (3.23) et (3.24), nous avons remarqué que l'on ne
pouvait pas les dissocier, car on ne les retrouve que sous la forme (á
+qb1).
Ceci étant, si le choix du couple (Xp,
Yp) et á a été accompli, alors, nous
calculerons qb1 et qb2 comme suit :
qb1=arctan2(A2-a2
SinA3-Yp ,
A1-a2CosA3-Xp)-á
qb2=A3-arctan2(A2-a2SinA3-Yp
, A 1-a2CosA3- Xp)
Par conséquent, l'ensemble des configurations [XP
YP á]T (représentants celle de la plateforme) qui
sont solutions du MGI, pour une situation imposée A=[A1 A2
A3]T de l'OT dans RA= (O A ,x
A , y A )
r r forment un cylindre
Sp(A) défini par l'équation (3.28) , ceci
implique
que pour chaque point de Sp(A), il existe une
paire (qb1,qb2) pour laquelle la situation de
l'OT dans RA est [A1 A2 A3]T.
Dans ce qui suit, nous allons construire le modèle
cinématique, où nous mettrons en évidence l'utilité
de la configuration du système mobile.
· Modèle Cinématique
En considérant que les coordonnées du point
Ob0 (a,b) sont quelconques, le modèle cinématique
direct de notre robot manipulateur mobile sera dit réduit, à
cause des contraintes non holonomes qui se présentent par rapport
à la plateforme mobile.
Nous avons évoqué précédemment le
modèle différentiel direct réduit, il est défini
comme étant l'application linéaire J telle que :
A&=J.p &
La mise en oeuvre de ce type de modèle est
étroitement liée aux contraintes non holonomes. Pour notre
plateforme mobile, les différentielles de la situation de la plateforme
[X& P Y & P á
& ]T sont dépendantes, elles sont liées par
çp. On peut faire intervenir une forme
différentielle p&
dont le nombre de composantes qui sont indépendantes
correspond au degré de mobilité du
système
mécanique. Il suffit de choisir : p& =
[p&1 p&2 ... p&Ddm ]T , le
choix des composantes du
vecteur p& est lié au type de bras et de
plateforme à traiter, donc, pour notre système, nous
considérons que le degrés de mobilité du manipulateur
mobile étudié est :
Ddm=Ddmp+ Ddmb =1+2=3.
Nous allons donc avoir : p& =[
p& 1 p&2
p & 3 ]T=[ q & b1 q &
b2 ç p ]T .
Le modèle cinématique en situation de notre
manipulateur mobile lie le vecteur des vitesses
opérationnelles
A& , aux vitesses généralisées du
bras ( q & b1 , q & b2) ainsi qu'à la
commande de
mobilité çp de la plateforme.
La matrice jacobienne réduite va être représentée en
considérant le modèle cinématique en situation de la
plateforme selon l'équation (3.2 1)
Le représentation p &nous mène
à calculer le modèle différentiel réduit, qui est
présenté dans ce qui suit où J(q b1, q b2
,á,â3) représente la matrice jacobienne réduite
de notre système :
|
?
?
?
?
?
|
&
A1
&
A2
&
A3
|
1
?
?
? J
|
J11
J21
1
) Ò ?
? J
? ?
? ?
? ?
? ?
&
qb1
&
q b2
çp
1 ? ?
? J
)
|
a S( q )
á +
1 b1
|
J a S( q q ) S(
12 2 b 1 b2 3
- á â
|
)C(á
|
)
|
C( )
â
+ +
3 (aS( )
á
L
|
bC(á
|
)
|
? C( )
â
= a C( q ) J a C( q q ) S( )S( )
+ - - +
3
1 b1 22 2 b1 b 2 3
á á â á (aC( ) bS( )
á á
? L

C()
â 3
1 1
L
J
(q q , )
b 1 b2 3
, , á â
Sachant que S représente le sinus et
C représente le cosinus, S(áqb1) et
C(áqb1) sont les sinus et cosinus de l'angle
(á+qb1), ainsi que
S(áqb1qb2) et
C(áqb1qb2) qui sont les sinus et cosinus de l'angle
á+qb1+qb2.
En étudiant la matrice J(q b 1 , q b2
,á,â3), nous remarquons que le degré de liberté
global de
notre système vaut uddl=3, il est
considéré comme non redondant cinématiquement puisque
Ddm-uddl=0. Si le choix des coordonnées
opérationnelles se portait uniquement sur les coordonnées en
position [XEA YEA]T, alors, uddl=2, ce
qui impliquera que le degré de redondance cinématique est
Ddm-uddl =1.
Le déterminant de la matrice jacobienne réduite est
:
a 1
Det( J(q b1 , q b 2 , á , â
3 ) )= -
(-aCos(â3)Sin(qb1)+LSin(â3)Cos(qb1)+bCos(â3)Cos(qb1)).
L
Le calcul du déterminant nous aide à
détecter les singularités du système à
étudier, cela se fera en considérant Det( J(q
b1 , qb2 ,á,â3 ) )=0. Nous remarquons pour notre
système que la détection des singularité se fera en
analysant les valeurs des variables liées au système telles que
a, b et L ; plusieurs cas se présentent :
b
-Si a=0 alors
LSin(â3)Cos(qb1)+bCos(â3)Cos(qb1)=0
â3=atan(- ) ou qb1 = ð +kð
(k? N).
L 2
-Si L=a et b=0,
Sin(â3)Cos(qb1)-Cos(â3)Sin(qb1)=0
â3=qb1+ kð(k? N).
Ces deux cas présentés sont les seuls
détectés analytiquement, les autres ne peuvent pas
apparaître aussi automatiquement, il faut user de méthodes
numériques pour déceler l'existence et les valeurs des
configurations singulières, en imposant les valeurs a,
b et L.
Pour ce qui est du modèle cinématique en
configurations, il sera déduit du modèle cinématique en
configurations de la plateforme comme suit :

&
qb
1
&
qb
2
&
?1
1 ? ? ? ? ? ? ? ? ?
? J
&
1
?
?
?
?
?
?
?
?
?
?
?
?
?
? J
0
Cos (â 3
)
-
0 0
0 0
Cos (â) Sin(â
3 3
-
r
0 0 Cos( )Sin(
á â 3
0 0 Sin( )Sin(
á â 3
L
0 1
10
01
1
D
(
00
L
r
1
D
(
00
L
r
00
Cos(â
3 3
) Sin(â
+
1
&
qb1
&
2
qb
çp
&
1
?
?
?
?
J
â3
00
00
)
)
))
))
0
0
0
0
0
?2
&
?3
&
Xp
&
Y p
&
á
&
â3
La paramètrisation des systèmes a son
importance, surtout par rapport au choix des coordonnées
opérationnelles (de la tâche) ; c'est un point
prépondérant car il influe sur la redondance. Cette
caractéristique peut aussi se révéler grâce à
l'ajout de la plateforme puisque pour le système de manipulation mobile
étudié, elle y est apparue (redondance
géométrique), alors qu'elle n'y avait pas existé
auparavant pour le système articulé seul. Cela implique que
l'ajout d'un véhicule mobile influe aussi sur le facteur de redondance
géométrique. De ce fait, nous pouvons déduire que
l'étude d'un manipulateur mobile diffère totalement de celle du
système articulé seul.
La construction de la matrice jacobienne d'un manipulateur
mobile est particulière, cela est dû principalement à la
cinématique du système à roues ; elle comprend dans sa
constitution les contraintes de roulement sans glissement qui changent d'un
type de plateforme à l'autre. Elle est également facteur de la
matrice partielle incluse par les vitesses articulaires du bras
embarqué.
Les calculs des différents modèles de
transformations d'espaces présentés dans ce chapitre se font en
suivant certaines règles générales pour un système
mobile quelconque, portant un type de bras ayant une structure à
chaîne cinématique ouverte, sans soucis du type d'articulation
qu'il comporte, ces principes de bases seront présentés dans le
prochain chapitre.
| 


