CHAPITRE I : GENERALITES SUR LES EQUATIONS
DIFFERENTIELLES ORDINAIRES ET LES EQUATIONS AUX DERIVEES PARTIELLES
1. LES EQUATIONS DIFFERENTIELLES ORDINAIRES
Définition I.1.1[9] une
équation différentielle est une relation entre la
variable   , une fonction inconnue , une fonction inconnue 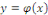 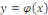 et ses dérivées et ses dérivées
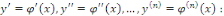
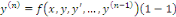
L'entier n s'appelle ordre de l'équation
différentielle 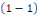 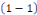
Définition 1.1.2 [9]
Intégrer l'équation différentielle 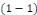 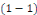 , c'est trouver toutes les fonctions , c'est trouver toutes les fonctions 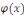 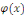 qui vérifient cette relation. qui vérifient cette relation.
Une telle fonction 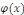 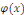 s'appelle solution, ou intégrale de l'équation s'appelle solution, ou intégrale de l'équation 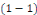 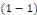 . Le graphe de la fonction . Le graphe de la fonction 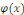 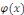 est appelé courbe intégrale de l'équation
différentielle est appelé courbe intégrale de l'équation
différentielle 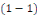 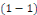 . .
Intégrer l'équation 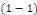 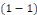 revient à trouver toutes les courbes intégrales. revient à trouver toutes les courbes intégrales.
Exemple 1.1.1
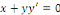 a) a) 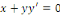 est une équation différentielle du 1er
ordre ; est une équation différentielle du 1er
ordre ;
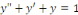 b) b) 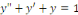 estune équation différentielle du 2ème
ordre. estune équation différentielle du 2ème
ordre.
I.1.1. EQUATIONS DIFFERENTIELLES DU PREMIER ORDRE [9]
Définition 1.1.3 une EDO est dite du premier
ordre, si elle est de la forme

Il y a trois classes principales d'équations
différentielles du premier ordre :
1° Equations à variables
séparables ;
2° Equations homogènes (où 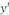 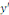 ne dépend que du rapport ne dépend que du rapport 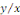 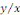 ) ; ) ;
3° Equations linéaires ( où 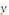 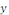 et et 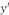 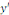 sont au premier degré). sont au premier degré).
Ces dernières peuvent être à coefficients
constants ou non, sans second membre ou avec second membre.
Exemples 1. 1. 2
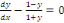 a. a. 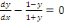 est une EDO à variables séparables du 1er
ordre ; est une EDO à variables séparables du 1er
ordre ;
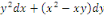 b. b. 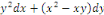 est une EDO homogène du 1er ordre ; est une EDO homogène du 1er ordre ;
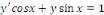 c. c. 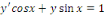 est une EDO linéaire du 1er ordre. est une EDO linéaire du 1er ordre.
EQUATIONS A VARIABLES SEPAREES 1.1.1.1
Définition 1.1.4 on appelle EDO à
variable séparées, toute EDO pouvant s'écrire :

Où   et et 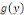 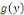 dépendent respectivement de dépendent respectivement de   et de et de   Puis on intègre les deux membres sans oublier la constante
d'intégration Puis on intègre les deux membres sans oublier la constante
d'intégration   , enfin, on se force de donner les solutions sous la forme explicite , enfin, on se force de donner les solutions sous la forme explicite
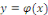
Exemple 1. 1. 3Soit l'EDO du premier ordre :
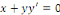 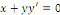
On l'écrit sous la forme 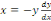 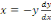
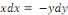 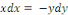
Soit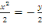 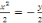 +c +c
ou encore 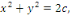 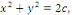 posons posons 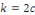 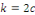
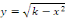
EQUATIONS HOMOGENES 1.1.1.2
Définition 1.1.5une EDO est dite
homogène lorsqu'on peut la mettre sous la forme :

Une telle EDO ne change pas lorsqu'on remplace   par par 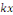 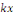 et et   par par 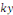 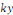 où où 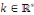 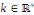 . .
RESOLUTION : on pose 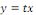 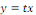 ou ou 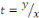 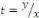 ou une nouvellefonction inconnue. ou une nouvellefonction inconnue.
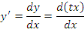
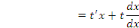
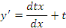
On sait que 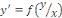 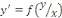
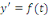
Remplaçons 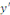 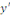 par sa valeur : par sa valeur :
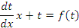
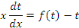
Séparons les variables
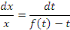
Intégrons membres à membre et obtenons
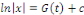
Ou
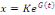
Portons cette dernière égalité dans 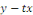 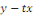 , on obtient , on obtient
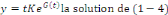
Exemple 1.1.4 soit à résoudre
l'équation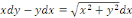 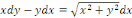 , une EDO Homogène du 1er ordre. , une EDO Homogène du 1er ordre.
Elle peut s'écrire sous la forme suivante :
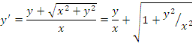
Posons 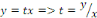 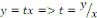 , d'où , d'où 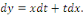 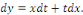 L'équation devient : L'équation devient :
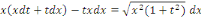
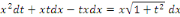 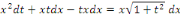
Ou en divisant par   et en supposant et en supposant 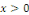 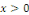 pour fixer les idées, pour fixer les idées,
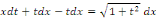
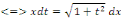
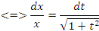
En intégrant membre à membre, on a :
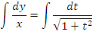
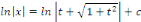
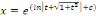
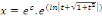
Posons 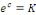 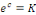
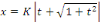
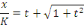
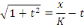
Elevons les deux membres au carré, pour exprimer   en fonction de en fonction de 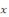 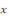 : :
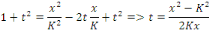
Puis que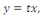 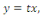 nous trouvons finalement : nous trouvons finalement :
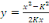 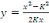 (c'est l'équation d'une formule de paraboles). (c'est l'équation d'une formule de paraboles).
| 


