EQUATIONS LINAIRES 1. 1. 1. 3
Définition 1. 1. 6une équation
différentielle linéaire du premier ordre est une
équation de la forme :

Où   et et   sont des fonctions continues de la variable sont des fonctions continues de la variable 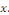 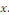
Lorsque le second membre 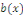 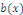 est nul, on dit que l'équation différentielle
linéaire est nul, on dit que l'équation différentielle
linéaire 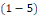 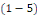 est sans second membre. est sans second membre.
Exemples 1. 1. 5
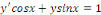 a. a. 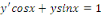 est une EDO linéaire du 1er ordre avec second
membre ; est une EDO linéaire du 1er ordre avec second
membre ;
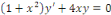 b. b. 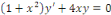 est une EDO linéaire du 1er ordre sans second
membre. est une EDO linéaire du 1er ordre sans second
membre.
A. EQUATION LINEAIRE SANS SECOND MEMBRE
Considérons l'équation

RESOLUTION : la résolution est très simple
car on se ramène au premier type d'équations du premier ordre
(à variables séparables) : on peut en effet séparer
les variables et l'intégration est immédiate.
Sachant que 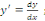 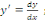
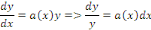
En intégrant membre à membre, on
obtient :
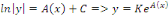
Posons 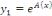 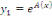 , une solution de l'équation homogène. , une solution de l'équation homogène.
Les solutions de l'équation 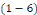 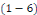 sont de la forme : sont de la forme :
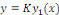 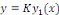 où où 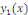 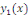 est une solution particulière non nulle de est une solution particulière non nulle de   qui est possible de calculer par quadrature. qui est possible de calculer par quadrature.
Exemple 1. 1. 6 soit à résoudre dans   l'EDO : l'EDO : 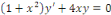 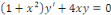
SOLUTION : Divisons l'EDO par 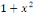 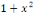 pour raison de normalisation pour raison de normalisation
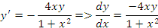
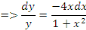
Intégrons membre à membre :
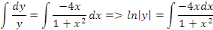
Du 2ème membre, posons 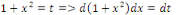 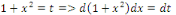
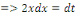
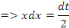
En remplaçant toujours dans le 2ème
membre, on obtient :
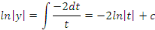
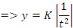
Or 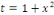 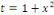 , alors , alors
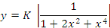
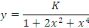
A. 1 EQUATION A COEFFICEINTS CONSTANTS
On se place dans le cas où   est une constante et l'équation est une constante et l'équation 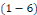 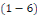 devient : devient :

RESOLUTION : 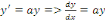 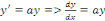
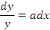
En intégrant membre à membre, on
obtient :
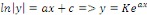 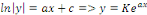 les solutions de les solutions de 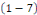 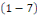 . .
Exemple 1. 1. 7 Soit à intégrer
dans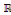 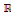 l'équation : l'équation :
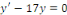
SOLUTION
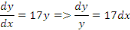
Intégrons membre à membre :
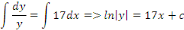
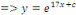
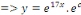
Posons 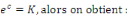 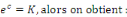
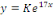
B. EQAUATION LINEAIRES AVEC SECOND MEMBRE
L'équation linéaire du premier ordre avec second
membre est de la forme :

SOLUTION posons 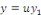 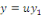 où où 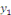 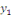 est la solution de l'équation est la solution de l'équation 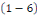 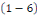 ici appelée équation associée à ici appelée équation associée à 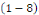 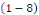
La fonction   est définie par est définie par
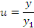
Ce changement de fonction revient à remplacer dans
l'expression 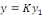 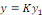 la constante la constante 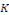 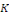 par une fonction variable par une fonction variable   , d'où le nom de variation de constante donné
à cette méthode. Elle consiste à calculer la
dérivée de , d'où le nom de variation de constante donné
à cette méthode. Elle consiste à calculer la
dérivée de
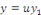 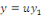 de la manière suivante : de la manière suivante :
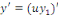
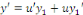
En remplaçant dans 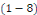 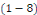 , on obtient : , on obtient :
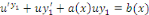
Puisque 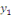 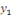 est la solution de l'équation est la solution de l'équation 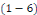 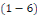 ,il reste donc à considérer ,il reste donc à considérer
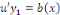
Ou 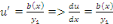 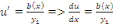
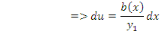
En intégrant membre à membre, on a :
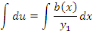
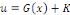
où 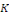 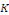 est une solution particulière. est une solution particulière.
Ceci étant, la solution générale s'en
déduit en multipliant les deux membres par 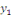 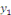 , c'est-à-dire : , c'est-à-dire :
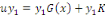
Or 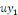 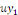 au départ était au départ était   , d'où : , d'où :
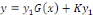
Exemple 1. 1. 8soit à intégrer
l'équation différentielle linéaire
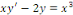
SOLUTION
En effet, l'équation homogène associée
est : 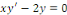 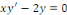
Séparons les variables :
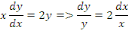
Intégrons membre à membre :
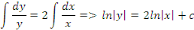
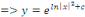
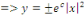
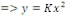
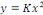 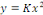 est la solution particulière de l'équation homogène
associée. est la solution particulière de l'équation homogène
associée.
Utilisons la méthode de variation de constante pour
trouver la solution générale :
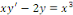 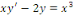 équation donnée équation donnée
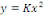 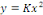 la solution de l'équation homogène associée. la solution de l'équation homogène associée.
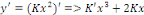
Portons ces dernières dans l'équation
donnée :
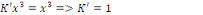
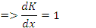
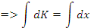
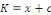
Portons les valeurs de 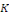 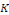 dans la solution homogène, on a : dans la solution homogène, on a :
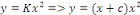
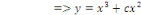 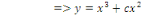 Solution générale de l'équation donnée. Solution générale de l'équation donnée.
C. EQUATION LINEAIRE A COEFFICIENTS ET SECOND MEMBRE
CONSTANTS
Dans ce cas, l'équation 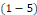 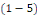 devient : devient :

Où   et et   sont deux nombres réels. sont deux nombres réels.
RESOLUTION : on peut dans ce cas séparer les
variables, en conservant le second membre :
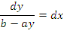
Intégrons : 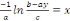 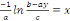
Multiplions les deux membres par 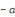 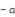 pour trouver pour trouver 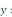 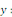
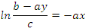
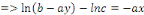
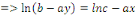
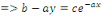
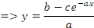
Exemple 1. 1. 9 Soit à intégrer
l'équation 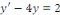 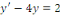
On peut écrire successivement
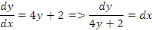
En intégrant, on obtient :
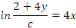
D'où, 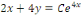 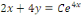
Et enfin 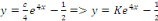 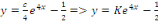 en posant en posant 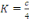 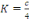
| 


