1. 2. EQUATIONS DIFFERENTIELLES DU SECOND ORDRE
Définition 1. 1. 7 [9]
une équation différentielle du deuxième ordre est de la
forme :

Il y a deux classes principales d'équations
différentielles du second ordre :
1. Equations incomplètes (se ramenant au premier
ordre) ;
2. Equations linéaires.
Exemples 1. 1. 10
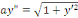 a. a. 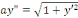 est une EDO du second ordre incomplète ; est une EDO du second ordre incomplète ;
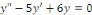 b. b. 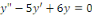 est un EDO linéaire du second ordre. est un EDO linéaire du second ordre.
EQUATION LINEAIRES DU SECOND ORDRE 1. 1. 2. 1. [2]
Définition 1. 1. 8 on appelle équation
linéaire du second ordre, toute équation de la forme :

Où 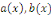 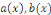 et et 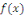 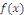 sont des fonctions continues sur l'intervalle I. sont des fonctions continues sur l'intervalle I.
Lorsque 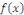 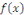 dans l'équation dans l'équation 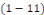 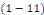 est nulle, alors l'équation se nomme : équation sans
second membre ou EDO linéaire homogène associée et
s'écrit sous la forme : est nulle, alors l'équation se nomme : équation sans
second membre ou EDO linéaire homogène associée et
s'écrit sous la forme :

Théorème 1. 1. 1La solution
générale de l'équation 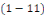 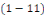 est la somme d'une solution particulière de cette
équation et de la solution générale de l'équation
homogène. est la somme d'une solution particulière de cette
équation et de la solution générale de l'équation
homogène.
Preuve : soit 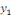 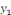 solution de l'équation complète. Posons solution de l'équation complète. Posons 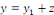 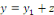 . .
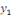 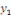 une la solution particulière et montrons que une la solution particulière et montrons que   est une solution de l'équation homogène ; pour y
arriver, cherchons les dérivées premières et secondes
de est une solution de l'équation homogène ; pour y
arriver, cherchons les dérivées premières et secondes
de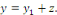 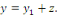
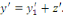
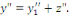
Portons les dérivées 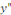 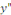 et et 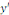 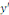 dans l'équation complète dans l'équation complète  
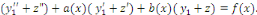
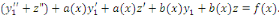
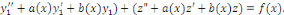
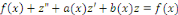
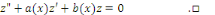
Donc   est une solution de l'équation homogène est une solution de l'équation homogène 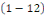 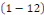 . .
EDO LINEAIRES HOMOGENES A COEFFICIENTS CONSTANT 1. 1. 2. 2.
[1]
Définition 1. 1. 9 Une EDO linéaire
homogène du second ordre est dite à coefficients constants si
elle est de la forme :

Où 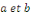 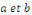 sont des réels. sont des réels.
Intégrer l'équation 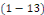 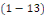 , c'est chercher s'il existe des intégrales de la forme , c'est chercher s'il existe des intégrales de la forme 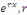 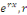 étant constant ; nous avons : étant constant ; nous avons :
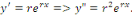
En portant 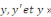 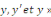 dans l'équation dans l'équation   , nous obtenons en divisant par , nous obtenons en divisant par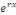 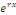 l'équation du second degré en l'équation du second degré en 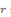 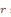

Appelée équation caractéristique de
l'équation 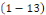 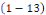
D'où, pour cette dernière, trois cas sont
possibles :
1. Si 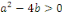 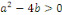 , l'équation , l'équation 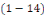 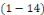 admet deux solutions distinctes admet deux solutions distinctes 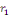 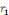 et et 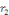 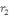 , les fonctions , les fonctions 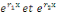 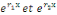 sont deux intégrales dont le rapport sont deux intégrales dont le rapport 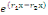 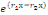 n'est pas constant. n'est pas constant.
Les intégrales sont de la forme :
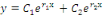
Où 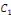 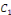 et et 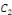 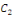 sont deux constantes arbitraires. sont deux constantes arbitraires.
2. Si 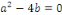 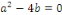 , l'équation , l'équation   admet une racine réelle double admet une racine réelle double 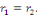 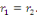
Les intégrales sont de la forme :
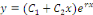
3. Si 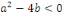 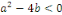 , alors l'équation , alors l'équation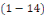 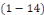 admet deux racines complexes admet deux racines complexes
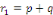 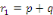 et et 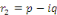 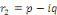
Les intégrales sont de la forme :
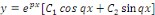
Exemples 1. 1. 11Soit à intégrer les
EDO linéaires suivantes :
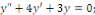 a. a. 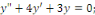
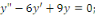 b. b. 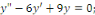
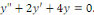 c. c. 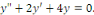
SOLUTIONS
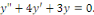 a. a. 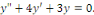 L'équation caractéristique est L'équation caractéristique est 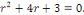 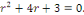
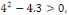 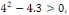 L'équation caractéristique admet deux racines
réelles : L'équation caractéristique admet deux racines
réelles :
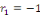 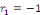 et et 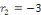 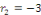 . Les intégrales de l'EDO sont de la forme : . Les intégrales de l'EDO sont de la forme :
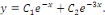
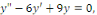 b. b. 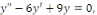 l'équation caractéristique est l'équation caractéristique est 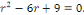 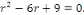
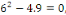 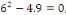 L'équation caractéristique admet un racine réelle
double. L'équation caractéristique admet un racine réelle
double.
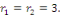
L'expression générale des intégrales
est :
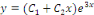
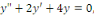 c. c. 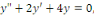 a pour équation caractéristique a pour équation caractéristique 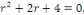 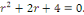
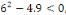 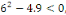 L'équation admet deux racines complexes : L'équation admet deux racines complexes :
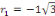 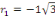 et et 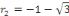 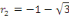
D'où, l'expression générale des
intégrales est :
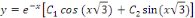
| 


