EDO LINEAIRES NON HOMOGENES A COEFFICIENTS
CONSTANTS : 1. 1. 2. 3. [1]
Soit l'équation
  . .
La solution générale de cette équation
est une combinaison linéaire de la solution de l'équation
homogène associée à 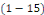 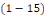 et d'une solution particulière. et d'une solution particulière.
Cette solution particulière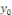 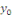 se détermine facilement par la méthode des coefficients
indéterminés dans les cas simples suivants : se détermine facilement par la méthode des coefficients
indéterminés dans les cas simples suivants :
1°. 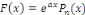 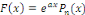 où où 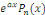 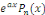 est un polynôme de degré est un polynôme de degré 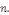 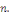
Ø Si 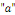 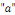 n'est pas une racine de l'équation caractéristique, alors
on pose : n'est pas une racine de l'équation caractéristique, alors
on pose :
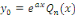 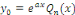 , où , où 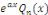 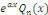 est un polynôme à déterminer ; est un polynôme à déterminer ;
Ø Si 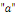 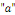 est une racine d'ordre « n » de l'équation
caractéristique, on pose : est une racine d'ordre « n » de l'équation
caractéristique, on pose :
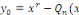 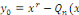 ). ).
2°. 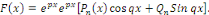 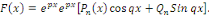
Ø Si 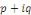 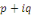 n'est pas racine de l'équation caractéristique, alors on
pose : n'est pas racine de l'équation caractéristique, alors on
pose :
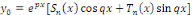 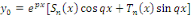 où où 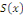 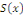 et et 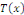 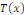 sont des polynômes de degré sont des polynômes de degré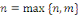 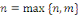 . .
Ø Si 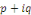 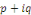 est une solution de l'équation caractéristique, alors on
pose : est une solution de l'équation caractéristique, alors on
pose :
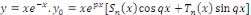
Exemple 1. 1. 12Soit à intégrer l'EDO
linéaire :
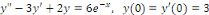
RESOLUTION : l'équation homogène
associée est
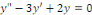
Son équation caractéristique est : 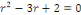 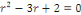
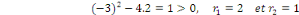 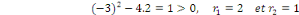 Alors, Alors,
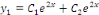 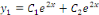 est la solution générale de l'équation
homogène. est la solution générale de l'équation
homogène.
Cherchons maintenant la solution particulière 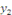 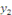 . .
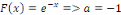
Posons 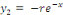 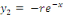 ceci implique ceci implique 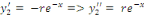 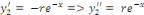
Portons 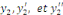 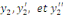 dans l'équation initiale : dans l'équation initiale :
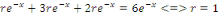
Connaissant la valeur de 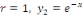 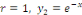
Pour trouver la solution générale, nous
prenons :
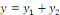
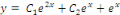
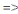
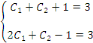
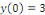
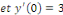
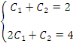
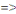
La solution particulière : 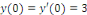 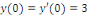
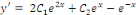
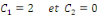
D'où, la solution générale est 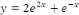 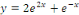
| 


