2. EQUATIONS AUX DERIVEES PARTIELLES
Définition 1.2.1 [5] une
équation aux dérivées partielles (EDP) est une
équation fonctionnelle qui met en relations les dérivées
partielles.
Typiquement, si   est une fonction à valeurs scalaires des variables est une fonction à valeurs scalaires des variables 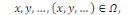 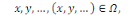 où où  désigne un ouvert de désigne un ouvert de 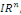 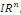 une EDP est une relation de la forme : une EDP est une relation de la forme :
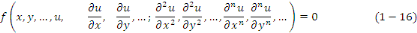
Pour 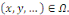 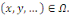
Où   désigne une fonction définie sur un ouvert de désigne une fonction définie sur un ouvert de 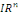 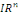
I.2. 1 DEFINITION DES CONCEPTS DE BASE [10]
Définition 1. 2. 2 L'ordre d'une
équation aux dérivées partielles est le plus haut
degré de dérivation présent dans l'équation 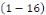 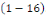
Définition 1. 2. 3La dimension d'une
équation aux dérivées partielles est le nombre de
variables indépendantes dont dépend la fonction inconnue 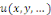 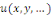 de de 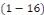 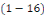 . .
Définition 1. 2. 4Résoudre une EDP
consiste donc à déterminer toutes les fonctions   définies sur le domaine définies sur le domaine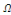 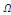 satisfaisant l'équation satisfaisant l'équation 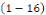 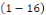
Exemple 1. 2. 1 Soit l'équation : 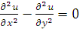 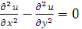
Est une EDP du second ordre et de dimension 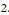 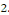
Les fonctions 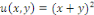 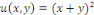 et et 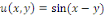 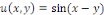 sont toutes des solutions de l'équation donnée dans
l'exemple 1.2.1 sont toutes des solutions de l'équation donnée dans
l'exemple 1.2.1 
Exemple 1. 2. 2 Soit l'EDP : 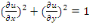 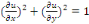
C'est une équation est une EDP du premier ordre et de
dimension deux (2).
Définition : 1. 2. 5. Une équation aux
dérivées partielles est du premier ordre si elle est de la
forme :

Où   est une fon,ction de plusieurs variables indépendantes est une fon,ction de plusieurs variables indépendantes 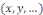 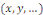 et des dérivées particulières du premier
ordre : et des dérivées particulières du premier
ordre :
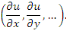
Exemple 1. 2. 3
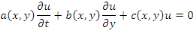
Est une EDP de transport.
2. 2 EDP LINEAIRES DU SECOND ORDRE [5]
Définition 1. 2. 6 Une équation aux
dérivées partielles est linéaire par rapport
à la fonction inconnue   et ses dérivées partielles. On peut l'écrire sous
la forme : et ses dérivées partielles. On peut l'écrire sous
la forme :

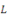 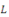 : est l'opérateur (application) linéaire aux
dérivées partielles associé à une EDP. : est l'opérateur (application) linéaire aux
dérivées partielles associé à une EDP.
Définition 1. 2. 7 On dit qu'une
équation aux dérivées partielles du second ordre est
linéaire si la dépendance par rapport à la fonction
inconnue   et ses dérivées partielles est linéaire : et ses dérivées partielles est linéaire :
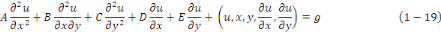
Remarque 1. 2. 1 Si 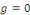 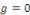 , alors l'équation , alors l'équation 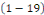 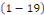 est dite homogène. est dite homogène.
Définition 1. 2. 8 On dit qu'une EDP est
semi-linéaire si la dépendance par rapport aux
dérivées partielles d'ordre le plus élevé est
linéaire, c'est-à-dire :
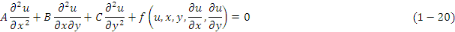
Définition 1. 2. 9 On dit qu'une EDP est
quasi-linéaire si elle est de la forme :
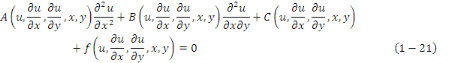
Définition 1. 2. 1 On dit qu'une EDP est
complétement non-linéaire si elle dépend
non-linéairement de ses termes d'ordre le plus élevé.
Exemple 1. 2. 4 Soit à montre la
linéarité de l'EDP
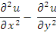
On sait que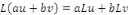 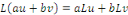
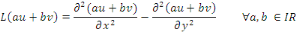
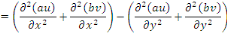
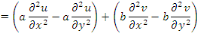
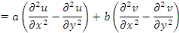

Donc, l'équation de l'exemple 1. 2. 1. Est
linéaire. Elle est du second ordre, de dimension 2 et
homogène.
Théorème 1. 2. 1
1. Si la fonction   est une solution de l'équation est une solution de l'équation 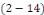 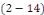 , et , et   solution de l'équation homogène associée,
alors solution de l'équation homogène associée,
alors 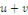 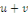 est solution de est solution de 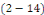 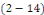 . .
2. Si 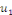 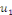 est solution de est solution de 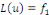 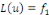 et et 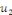 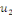 solution de solution de 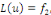 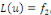 alors alors 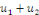 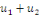 est solution de est solution de 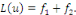 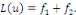
Preuve :
1. Comme 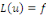 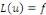 et et 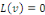 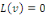
Donc : 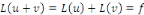 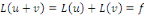 car la linéarité de car la linéarité de 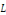 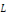 . .
Alors 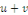 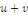 est solution de est solution de 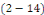 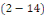 . .
2. Nous savons que 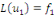 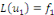 et que et que 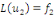 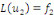
Par conséquent, 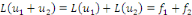 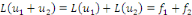
Nous avons donc 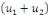 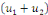 est solution de est solution de 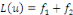 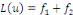 .? .?
Théorème 1. 2. 2La solution
générale d'une équation différentielle
linéaire d'ordre   dépend linéairement de dépend linéairement de   fonctions arbitraires. fonctions arbitraires.
Exemple 1. 2. 5 Soit l'EDP linéaire
homogène :
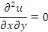
En intégrant par rapport à y, on
obtient :
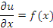
En intégrant par rapport à x et en notant 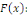 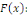 un primitive de la fonction arbitraire un primitive de la fonction arbitraire 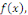 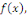 on obtient : on obtient :
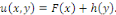
les fonctions 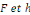 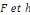 sont deux fonction quelconques. sont deux fonction quelconques.
| 


