2. 3CLASSIFICATION DES EDP DANS 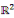 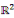
Définition 1. 2. 11 [11] On
appelle généralement équation aux dérivées
partielles linéaires d'ordre inférieur ou égal à
deux (2) dans un domaine ??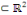 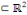 et d'inconnue et d'inconnue 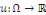 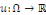 une équation du type : une équation du type :
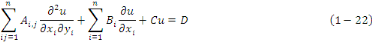
Par convention, on supposera que 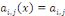 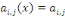 avec avec 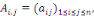 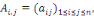 la matrice la matrice
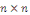 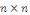 symétrique de coefficients devant les termes d'ordre 2. symétrique de coefficients devant les termes d'ordre 2.
Soit
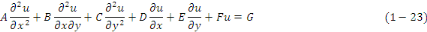
Où 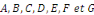 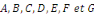 sont des fonctions de sont des fonctions de 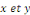 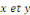 qui ne s'annulent pas simultanément qui ne s'annulent pas simultanément  . .
Nous supposerons aussi que 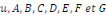 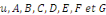 sont toutes au moins des dérivées d'ordre sont toutes au moins des dérivées d'ordre 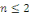 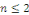 continues sur le domaine continues sur le domaine   du plan (x, y). du plan (x, y).
D'où, de l'équation 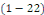 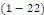 , on chercher des valeurs propres de la matrice , on chercher des valeurs propres de la matrice 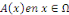 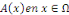 et de l'équation et de l'équation 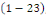 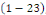 on cherchera le discriminant on cherchera le discriminant   pour déterminer de quel type d'EDP linéaire du second
ordre il s'agit. pour déterminer de quel type d'EDP linéaire du second
ordre il s'agit.
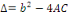
Pour toutes ces deux formes 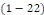 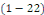 et et 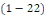 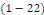 d'équation aux dérivées partielles, il existe
trois (3) types d'EDP linéaire du second ordre : d'équation aux dérivées partielles, il existe
trois (3) types d'EDP linéaire du second ordre :
EDP du type hyperbolique, du type parabolique et du type
elliptique. 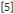
Remarque 1. 2. 2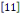 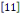 Suite à la définition 1. 2. 11, avant la matrice Suite à la définition 1. 2. 11, avant la matrice   est définie sous cette forme : est définie sous cette forme :
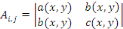
Alors, le polynôme caractéristique de cette
matrice :
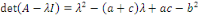
Donc, il y a deux valeurs propres 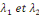 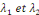 avec avec
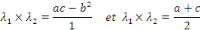
1. EDP DU TYPE HYPERBOLIQUE 
Définition 1. 2. 12  Soit l'équation telle que Soit l'équation telle que  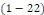 ou ou 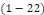 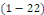 dans un domaine dans un domaine   . .
Lorsque 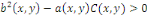 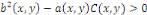
Ou 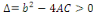 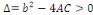 , elle est dite du type hyperbolique dans ce domaine. , elle est dite du type hyperbolique dans ce domaine.
Remarque 1. 2. 3  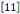 : on dit qu'une équation est du type hyperbolique si les valeurs
propres sont non nulles et de même signe sauf une, alors : on dit qu'une équation est du type hyperbolique si les valeurs
propres sont non nulles et de même signe sauf une, alors
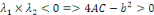 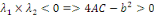 et ce qui donne et ce qui donne 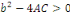 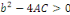
Exemple 1. 2. 6 (EDP des ondes) soit 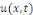 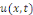 une fonction des variables d'espace une fonction des variables d'espace   et du temps et du temps   , définie sur un domaine , définie sur un domaine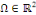 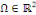 et pour et pour   positif. positif.
L'équation des ondes pour la fonction   s'écrit : s'écrit :
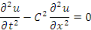
Par identification, 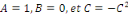 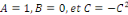
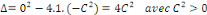
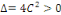
L'EDP des ondes est donc du type hyperbolique.
1. EDP DU TYPE PARABOLIQUE
Définition 1. 2. 13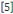 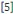 Soit l'EDP telle que Soit l'EDP telle que 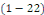 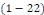 ou ou 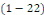 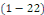 dans un domaine dans un domaine   Lors que Lors que  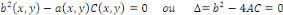
Elle est dite parabolique dans ce domaine.
Remarque 1. 2. 4 On dit que l'EDP est du type
parabolique en 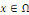 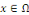 si si 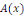 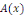 admet admet 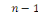 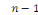 valeurs propres de même signe et une valeur propre nulle. valeurs propres de même signe et une valeur propre nulle.
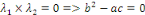
Ou encore 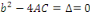 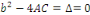
Exemple 1. 2. 7 (EDP de la chaleur). Soit 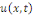 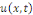 des variables d'espace des variables d'espace   et du temps et du temps 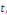 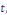 définie sur un domaine définie sur un domaine   de de 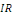 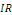 et pour et pour   positif. positif.
L'équation de la chaleur pour la fonction  s'écrit : s'écrit :
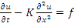 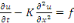 avec avec   donné. donné.
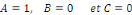 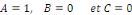 par identification. par identification.
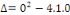
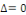
L'équation de la chaleur est donc du type
parabolique.
1. EDP DU TYPE ELLIPTIQUE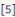 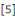
Définition 1. 2.14 Soit
l'EDP telle que 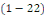 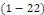 ou ou 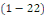 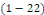 dans un domaine dans un domaine 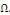 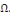
Lors que 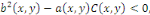 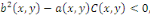
Elle est dite du type elliptique dans ce domaine.
Remarque 1.2.5Une EDP est du type elliptique en 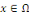 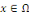 si la matrice si la matrice 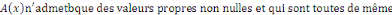 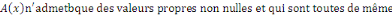 signe : signe :
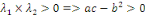
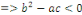
Exemple 1. 2. 8 (EDP de Laplace) soit 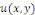 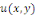 une fonction définie sur un domaine une fonction définie sur un domaine 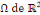 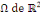 et vérifiant dans ce domaine l'équation de
Laplace : et vérifiant dans ce domaine l'équation de
Laplace :
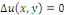 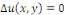 ou ou
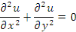
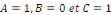 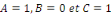 par identification par identification
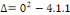
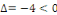
L'équation de Laplace est donc du type elliptique.
| 


