I.2.4. SYSTEME ORTHOGONAL [11]
Soit les fonctions 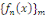 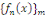 continues sur l'intervalle continues sur l'intervalle 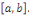 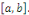
Nous dirons que 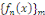 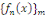 est un système orthogonal sur est un système orthogonal sur 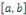 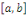 si et seulement si : si et seulement si :
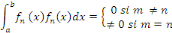
La section constante de séparation de la
dernière égalité
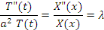
Dont le premier membre dépend de 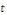 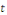 seul et le second de seul et le second de 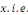 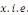 sont égaux à une même constante que nous
désignons sont égaux à une même constante que nous
désignons 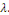 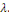
I.2.5. PROBLEME BIEN POSE [6]
Définition 1. 2. 15 En mathématique, un
problème est bien posé s'il a une solution et cette solution est
unique.
Soit une EDP valide dans un domaine   , munie de conditions aux frontières. Le problème est bien
posé si (s') : , munie de conditions aux frontières. Le problème est bien
posé si (s') :
v Il existe une solution de l'EDP satisfaisant les conditions
aux frontières (existence) ;
v La solution est unique (unicité) ;
v La solution est stable par rapport aux conditions aux
frontières imposées (stabilité).
TABLEAU RECAPITULATIF [6]
Pour une EDP du second ordre linéaire à
coefficients constants, on a un problème bien posé dans les cas
suivants (conditions suffisantes) :
|
TYPE
|
FRONTIERE
|
CONDITION
|
|
Hyperbolique
|
Ouverte
|
Cauchy
|
|
Parabolique
|
Ouverte
|
Dirichlet ou Neumann
|
|
Elliptique
|
Fermée
|
Dirichlet ou Neumann
|
| 


