I.2. 6. CONDITION SUR L'ENSEMBLE DES SOLUTIONS [6]
Pour trouver des solutions particulières aux EDP
à partir de la solution générale, on impose des conditions
restrictives sur l'ensemble des solutions.
Les conditions les plus fréquentes sont :
1. CONDITION INITIALES
Si   est une fonction de est une fonction de 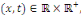 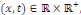 on donne on donne
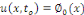 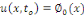 ou ou 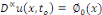 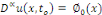 , on parle aussi des conditions de Cauchy. , on parle aussi des conditions de Cauchy.
2. CONDITIONS AUX LIMITES
Définition 1. 2. 16Une condition aux limites
est une contrainte sur les valeurs que prennent les solutions des EDP sur une
frontière.
Ces conditions imposent une valeur de la fonction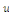 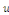 ou de ses dérivées partielles au bord du domaine ou de ses dérivées partielles au bord du domaine   . .
Il existe plusieurs types de conditions aux limites dont nous
citons quelques-unes :
v Condition de Dirichlet : où on impose la valeur
de la fonction recherchée sur le bord 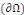 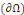
Exemple 1. 2. 9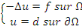 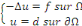
Où   est une fonction. si est une fonction. si 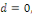 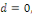 on qualifiera le problème d'homogène, dans le cas
contraire il sera dit non homogène. on qualifiera le problème d'homogène, dans le cas
contraire il sera dit non homogène.
v Condition de Neumann : où on impose la valeur de
la dérivée normale de la fonction recherchée sur le bord
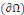 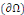 . .
Exemple 1. 2. 10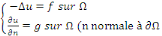 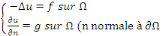 où où   est une fonction est une fonction
Un problème du 2ème type est un celui
où tout le bord est soumis à des conditions de Neumann.
v Conditions de Fourier-Robin : où on impose une
relation entre la valeur de la dérivée normale de la fonction
recherchée et sa valeur sur le bord (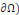 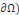 . .
Exemple1.2.11 On note 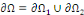 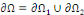
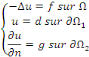
Un problème du 3ème type est celui
où les conditions sont des types différents sur des portions de
bord 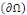 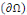
v Conditions Périodiques :
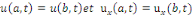
| 


